Beispiele für die Arbeit mit Maxima
Hier werden Beispiele gezeigt, wie mit dem Computeralgebrasystem
Maxima Aufgaben bearbeitet werden können. Die Beispiele entsprechen einer
Vorlesung für Naturwissenschaftler, die zwei Semester Mathematik belegen
müssen.
Die Beispiele wurden vollständig mit wxMaxima erstellt und aus wxMaxima
nach HTML exportiert.
Auswahl der Kapitel
2 Ableitung von Funktionen
Beispiel 1: Ableitung als Grenzwert des Differenzenquotienten
Zu Beginn der Sitzung löschen wir eventuell vorhandene Variablen und Funktionsdefinitionen mit der Funktion kill.
| (%i1) | kill(all)$ |
Wir zeigen die Definition des Differenzenquotienten in der Schreibweise von Maxima.
Die Funktion limit bildet den Grenzert. Das erste Argument ist der Ausdruck für den der Grenzwert bestimmt werden soll. Es folgen die Grenzwertvariable und der Wert gegen den die Variable gehen soll.
| (%i1) | limit((f(x+h)-f(x))/h, h, 0); |
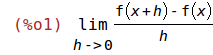
Im folgenden definieren wir jeweils die Funktion und bilden dann den Differenzenquotienten.
| (%i2) | f(x):=x^2$ |
| (%i3) | limit((f(x+h)-f(x))/h, h, 0); |

| (%i4) | f(x):=sqrt(x)$ |
| (%i5) | limit((f(x+h)-f(x))/h, h, 0); |

| (%i6) | f(x):=10/x$ |
| (%i7) | limit((f(x+h)-f(x))/h, h, 0); |

| (%i8) | f(x):=3*x^3$ |
| (%i9) | limit((f(x+h)-f(x))/h, h, 0); |

Beispiel 2: Summenregel
Für die folgenden Funktionen ist die Summenregel der Ableitung anzuwenden.
Die Summenregel wie sie Maxima in einer symbolischen Schreibweise anwendet.
| (%i10) | f(x):=u(x)+v(x)$ |
Die Ableitung wird mit der Funktion diff gebildet. Das erste Argument ist die Funktion und das zweite Argument die Variable.
| (%i11) | diff(f(x),x); |
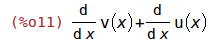
Hinweis: Höhere Ableitungen und partielle Ableitungen sind ebenfalls möglich. Das folgende Beispiel zeigt ein Beispiel für die Schreibweise.
| (%i12) |
kill(f)$ diff(f(x,y),x,2,y,3); |

Die folgenden Beispiele zeigen die Ergebnisse für die erste Ableitung verschiedener Funktionen.
| (%i14) | f(x):=4*x^5 + x^(1/3) + a^10$ |
| (%i15) | diff(f(x), x); |
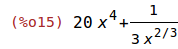
| (%i16) | f(x):= exp(x) - sin(x) + cos(x)$ |
| (%i17) | diff(f(x), x); |
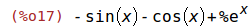
| (%i18) | f(x):= a^n*x^n + b^(n-1)*x^(n-1) + c*n$ |
| (%i19) | diff(f(x), x); |
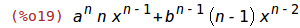
Beispiel 3: Kettenregel
In den folgenden Beispielen wendet Maxima die Kettenregel an.
| (%i20) | f(x):= sin(2-x^3+3*x^4)$ |
| (%i21) | diff(f(x), x); |
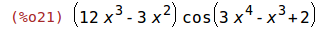
| (%i22) | f(x):= exp(x^2+3*x)$ |
| (%i23) | diff(f(x), x); |
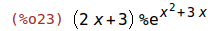
| (%i24) | f(x):= log(cos(x^2))$ |
| (%i25) | diff(f(x), x); |
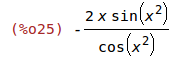
Beispiel 4: Produktregel
Anwendung der Produktregel für die Ableitung von Funktionen.
Zunächst die Produktregel in der symbolischen Schreibweise von Maxima.
| (%i26) | f(x):= u(x) * v(x)$ |
| (%i27) | diff(f(x), x); |
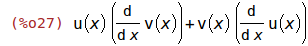
Beispiele für die Anwendung der Produktregel für die Ableitung von Funktionen.
| (%i28) | f(x):= exp(x)*sin(x)$ |
| (%i29) | diff(f(x), x); |

| (%i30) | f(x):= x^2*sqrt(3*x)$ |
| (%i31) | diff(f(x), x); |

| (%i32) | f(x):= 7*x^(1/3)*log(x)$ |
| (%i33) | diff(f(x),x); |
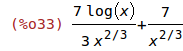
Beispiel 5: Quotientenregel
Beispiele für die Anwendung der Quotientenregel.
Die Quotientenregel in der symbolischen Schreibweise von Maxima.
| (%i34) | f(x):= u(x)/v(x)$ |
Das Ergebnis wird mit der Funktion ratsimp vereinfacht, um ein Ergebnis zu erhalten, dass der bekannten Lehrbuchformel ähnelt. Maximas Ergebnis unterscheidet sich durch die Reihenfolge der Terme im Nenner des Ausdrucks von einer Lehrbuchformel.
| (%i35) | diff(f(x), x),ratsimp; |
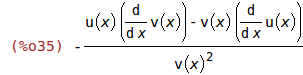
Beispiele für die Anwendung der Quotientenregel für die Ableitung von Funktionen.
| (%i36) | f(x):= log(x)/x^2$ |
| (%i37) | diff(f(x), x); |

| (%i38) | f(x):= sqrt(x)/(x+1)^2$ |
| (%i39) | diff(f(x), x); |
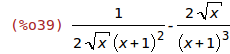
| (%i40) | f(x):= exp(2*x)/(x-1)$ |
| (%i41) | diff(f(x), x); |

Beispiel 6: Gemischte Ableitungen
| (%i42) | f(x):= log(log(log(x)))$ |
| (%i43) | diff(f(x), x); |
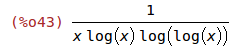
| (%i44) | f(x):= x^2*cos(x)/(x+1)$ |
| (%i45) | diff(f(x), x); |

| (%i46) | f(x):= exp(x*sin(x))$ |
| (%i47) | diff(f(x), x); |
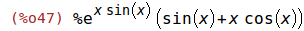
| (%i48) | f(x):= log(2*x)*sin(sqrt(x^2+1))$ |
| (%i49) | diff(f(x), x); |
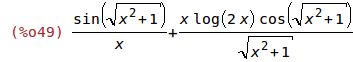
Beispiel 7: Ableitung der Umkehrfunktion
Wir definieren die Funktion y(x) = x^(1/6) als eine Gleichung und nehmen an, dass y>0 ist.
| (%i50) |
assume(y>0)$ eqn: y=x^(1/6); |
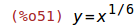
Wir lösen die Gleichung mit der Funktion solve nach x auf. An dieser Stelle benötigt die Funktion solve die Information, dass y>0 ist.
| (%i52) | solve(eqn, x); |
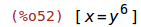
Mit der Funktion first bekommen wir das erste Element der obigen Liste. Das ist in diesem Fall unsere inverse Funktion. Dann differenzieren wir die rechte Seite der Gleichung und nehmen den Kehrwert.
| (%i53) | 1/diff(rhs(first(%)),y); |
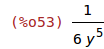
Zuletzt sustituieren wir die ursprüngliche Gleichung in das Ergebnis zurück und erhalten das gewünschte Ergebnis.
| (%i54) | subst(eqn,%); |

Das ist die Ableitung der ursprünglichen Funktion
| (%i55) | diff(x^(1/6), x); |
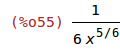
Zum Abschluss entfernen wir die Anname y>0.
| (%i56) | forget(y>0); |
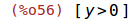
Ein weiteres Beispiel für die Ableitung der Umkehrfunktion.
| (%i57) | eqn: y = log(x); |
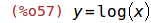
| (%i58) | solve(eqn, x); |
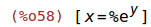
| (%i59) | 1/diff(rhs(first(%)), y); |

| (%i60) | subst(eqn, %); |

Zur Probe die direkte Ableitung.
| (%i61) | diff(log(x), x); |

Ein weiteres Beispiel für die Funktion y(x) = sqrt(exp(x)+1) mit y>0.
| (%i62) |
assume(y>0)$ eqn: y = sqrt(exp(x)+1)$ |
| (%i64) | solve(eqn, x); |
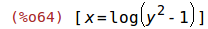
| (%i65) | 1/diff(rhs(first(%)), y); |
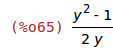
| (%i66) | subst(eqn, %); |
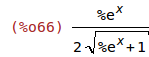
| (%i67) | forget(y>0)$ |
Zuletzt die Probe.
| (%i68) | diff(sqrt(exp(x)+1), x); |
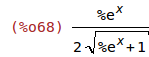
Beispiel 8: Implizite Ableitung
Wir suchen die implizite Ableitung der folgenden Funktion.
| (%i69) | eqn: x^2 + 2*y^2 =22$ |
Die Variable y ist von x anhängig. Wir definieren dies mit der Funktion depends.
| (%i70) | depends(y,x); |
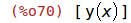
Jetzt können wir beide Seite der Gleichung ableiten. Die Ableitung von y tritt symbolisch als dy/dx auf.
| (%i71) | diff(eqn, x); |
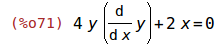
Die Ableitung der Gleichung wird mit der Funktion nach dy/dx aufgelöst.
| (%i72) | sol: solve(%,diff(y,x)); |

Die rechte Seite der Gleichung ist die Steigung.
| (%i73) | rhs(first(sol)); |

Zuletzt berechnen wir die Steigung der Tangente für den Punkt P(2,3), indem wir die Werte einsetzten.
| (%i74) | %, x=2, y=3; |

Beispiel 9: Implizite Ableitung
Bestimmen Sie die Steigung der Tangente an den Kreis um den Koordinatenursprung mit dem Radius r=5.
Die Kreisgleichung für einen Kreis um den Koordinatenursprung mit dem Radius r=5 ist:
| (%i75) | eqn: x^2 + y^2 = 5^2$ |
Wir gehen wir im letzten Beispiel vor und berechnen die implizite Ableitung, um die Steigung zu finden.
| (%i76) | depends(y,x); |
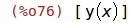
| (%i77) | diff(eqn, x); |
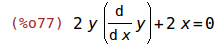
| (%i78) | sol: solve(%, diff(y,x)); |
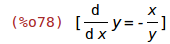
| (%i79) | rhs(first(sol)); |

| (%i80) | %, x=3, y=4; |

Created with wxMaxima.