Beispiele für die Arbeit mit Maxima
Hier werden Beispiele gezeigt, wie mit dem Computeralgebrasystem
Maxima Aufgaben bearbeitet werden können. Die Beispiele entsprechen einer
Vorlesung für Naturwissenschaftler, die zwei Semester Mathematik belegen
müssen.
Die Beispiele wurden vollständig mit wxMaxima erstellt und aus wxMaxima
nach HTML exportiert.
Auswahl der Kapitel
1 Rechnen mit komplexen Zahlen
Beispiel 1:
a) Bilden Sie die Summe, Differenz, das Produkt und den Quotienten der komplexen Zahlen:
z1 = 6 + 4*i und z2 = 5-2*i
z1 = -6 + i und z2 = 2-i
Die komplexen Zahlen werden den Variablen z1 und z2 mit dem Operator ":" zugewiesen.
Die imaginäre Einheit wird durch das Symbol %i dargestellt. Die Eingabe wird mit dem Zeichen $ abgeschlossen, um die Ausgabe zu unterdrücken.
| (%i1) |
z1 : 6+4*%i$ z2 : 5-2*%i$ |
Die Summe und die Differenz der komplexen Zahlen. In diesem Fall wird die Eingabe mit dem Zeichen ; abgeschlossen, um die Ergebnisse anzuzeigen.
| (%i3) |
z1+z2; z1-z2; |

Das Produkt wird nicht automatisch ausmultipliziert.
Dies gelingt mit der Funktion expand. Auf das letzte Ergebnis wird mit dem Operator % zugegriffen.
| (%i5) |
z1*z2; expand(%); |
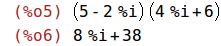
Auch der Quotient wird nicht automatisch ausgerechnet.
In diesem Fall wird die Funktion rectform eingesetzt, die einen komplexen Ausdruck in die Standardform bringt.
| (%i7) |
z1/z2; rectform(%); |

Dieselben Rechnungen für zwei weitere komplexe Zahlen.
In diesem Fall wenden wir die Funktionen expand und rectform sofort auf das Produkt z1*z2 und den Quotienten z1/z1 an.
| (%i9) |
z1 : -6+%i$ z2 : 2-%i$ |
| (%i11) |
z1+z2; z1-z2; |
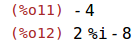
| (%i13) | expand(z1*z2); |
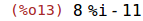
| (%i14) | rectform(z1/z2); |
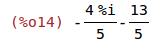
b) Skizzieren Sie die folgenden komplexe Zahlen sowie die zugehörigen konjugiert komplexen Zahlenn auf der komplexen Zahlenebene und rechnen Sie sie in die trigonometrische Form um.
z1 = -5 und z2 = (-1-i*sqrt(3))/2
z3 = 1-i und z4 = 2*i
Den Variablen z1 und z2 werden die komplexen Zahlen zugewiesen.
Mit der Funktion conjugate werden die konjugiert komplexen Zahlen berechnet. Die Ergebnisse werden den Variablen z1_ und z2_ zugewiesen.
| (%i15) |
z1 : -5$ z2 : (-1-%i*sqrt(3))/2$ z1_ : conjugate(z1); z2_ : conjugate(z2); |
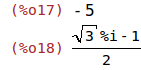
Mit der Funktion polarform erhalten wir die komplexen Zahlen z1 und z2 in der Polarform.
| (%i19) |
polarform(z1); polarform(z2); |

Mit der Funktion wxdraw2d können in wxMaxima die komplexen Zahlen als Vektoren in der komplexen Zahlenebene gezeichnet werden. Wird nicht wxMaxima verwendet, kann stattdessen die Funktion draw2d genutzt werden.
Die Syntax der Plot-Funktion kann sehr kompliziert sein und soll hier nicht weiter erläutert werden.
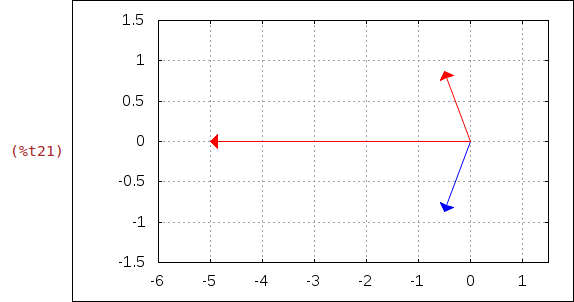
Die konjugiert komplexen Zahlen haben die Farbe rot im Diagramm. Da die Zahl z1 = -5 mit ihrer konjugiert komplexen Zahlen zusammenfällt, wird z1 im Diagramm von z1_ überdeckt.
Der Realteil und der Imaginärteil der komplexen Zahlen sind die Koordinaten des Vektors in der komplexen Zahlenebene. Diese werden mit den entsprechenden Maxima-Funktionen berechnet.
| (%i21) |
wxdraw2d( /* Schalte Gitter ein */ grid = true, /* x- und y-Bereich */ xrange = [-6,1.5], yrange = [-1.5,1.5], /* Stil des Vektors */ head_length = 0.2, line_type = solid, /* Komplex Zahlen als Vektor */ color = blue, vector([0,0],[realpart(z1),imagpart(z1)]), vector([0,0],[realpart(z2),imagpart(z2)]), color = red, vector([0,0],[realpart(z1_),imagpart(z1_)]), vector([0,0],[realpart(z2_),imagpart(z2_)]) )$ |
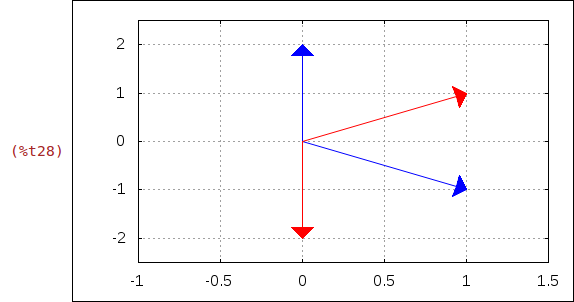
Die obigen Rechnungen werden für das zweite Paar komplexer Zahlen der Aufgabe wiederholt.
| (%i22) |
z1 : 1-%i$ z2 : 2*%i$ z1_ : conjugate(z1); z2_ : conjugate(z2); |

| (%i26) |
polarform(z1); polarform(z2); |
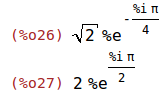
| (%i28) |
wxdraw2d( /* Schalte Gitter ein */ grid = true, /* x- und y-Bereich */ xrange = [-1,1.5], yrange = [-2.5,2.5], /* Stil für den Vektor */ head_length = 0.1, line_type = solid, /* Komplex Zahlen als Vektor */ color = blue, vector([0,0],[realpart(z1),imagpart(z1)]), vector([0,0],[realpart(z2),imagpart(z2)]), color = red, vector([0,0],[realpart(z1_),imagpart(z1_)]), vector([0,0],[realpart(z2_),imagpart(z2_)]) )$ |
Beispiel 2:
a) Berechnen Sie aus den gegebenen komplexen Zahlen z1 und z2 die folgenden Ausdrücke in der algebraischen Darstellung:
z1+z2, z1-z2, z1/z2 und z1*z2
z1 = 4*i und z2 = sqrt(3)+i
z1 = 2+5*i und z2 = 1+i
Die verwendeten Methoden und Funktionen wurden vollständig für die Aufgabe 1 erläutert. Für diese Aufgabe werden nur die Ergebnisse gezeigt.
| (%i29) |
z1:4*%i$ z2:sqrt(3)+%i$ |
| (%i31) |
z1+z2; z1-z2; |
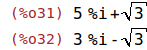
| (%i33) |
expand(z1*z2); rectform(z1/z2); |
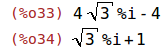
b) Skizzieren Sie diese Zahlen auf der komplexen Zahlenebene.
Diagramm mit den komplexen Zahlen z1, z2, z1+z2 und z1-z2.
| (%i35) |
wxdraw2d( /* Schalte Gitter ein */ grid = true, /* x- und y-Bereich */ xrange = [-2,2], yrange = [-1,6], /* Stil für den Vektor */ head_length = 0.1, line_type = solid, /* Komplex Zahlen als Vektor */ color = blue, vector([0,0],[realpart(z1),imagpart(z1)]), vector([0,0],[realpart(z2),imagpart(z2)]), color = red, vector([0,0],[realpart(z1+z2),imagpart(z1+z2)]), color = green, vector([0,0],[realpart(z1-z2),imagpart(z1-z2)]) )$ |
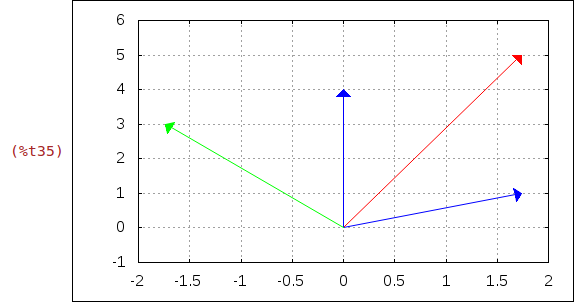
Diagramm mit den komplexen Zahlen z1, z2, z1*z2 und z1/z2.
| (%i36) |
wxdraw2d( /* Schalte Gitter ein */ grid = true, /* x- und y-Bereich */ xrange = [-5,2], yrange = [-1,8], /* Stil für den Vektor */ head_length = 0.1, line_type = solid, /* Komplex Zahlen als Vektor */ color = blue, vector([0,0],[realpart(z1),imagpart(z1)]), vector([0,0],[realpart(z2),imagpart(z2)]), color = red, vector([0,0],[realpart(z1*z2),imagpart(z1*z2)]), color = green, vector([0,0],[realpart(z1/z2),imagpart(z1/z2)]) )$ |
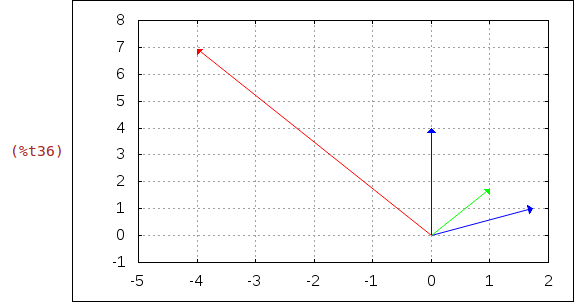
c) Rechnen Sie z1 und z2 in die trigonometrische Form um und berechnen Sie den Quotienten z1/z2 und das Produkt z1*z2.
| (%i37) |
z1:polarform(z1); z2:polarform(z2); |

Mit dem Schalter %emode wird verhindert, dass Maxima die Polarform vereinfacht.
| (%i39) |
z1*z2, %emode:false; z1/z2, %emode:false; |
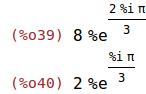
Wiederholung der obigen Rechnungen für ein weiteres Beispiel.
| (%i41) |
z1: 2+5*%i$ z2: 1+%i$ |
| (%i43) |
z1+z2; z1-z2; |

| (%i45) |
expand(z1*z2); rectform(z1/z2); |
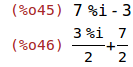
Diagramm für die komplexen Zahlen z1, z2, z1+z2 und z1-z2.
| (%i47) |
wxdraw2d( /* Schalte Gitter ein */ grid = true, /* x- und y-Bereich */ xrange = [-0.5,3.5], yrange = [-1,6.5], /* Stil für den Vektor */ head_length = 0.1, line_type = solid, /* Komplex Zahlen als Vektor */ color = blue, vector([0,0],[realpart(z1),imagpart(z1)]), vector([0,0],[realpart(z2),imagpart(z2)]), color = red, vector([0,0],[realpart(z1+z2),imagpart(z1+z2)]), color = green, vector([0,0],[realpart(z1-z2),imagpart(z1-z2)]) )$ |
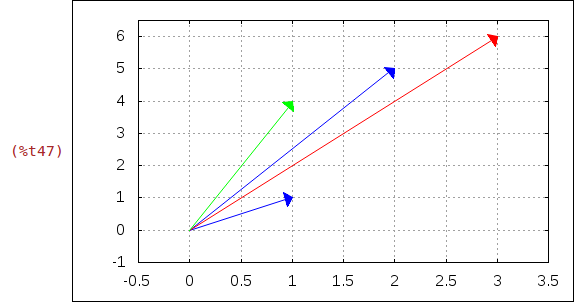
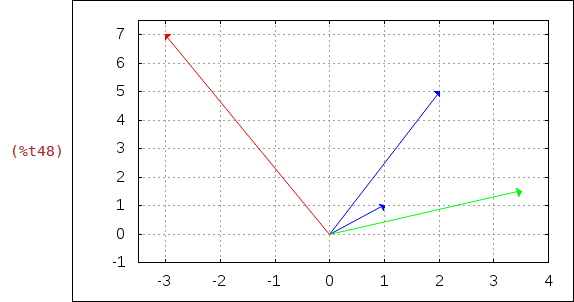
Diagramm für die komplexen Zahlen z1, z2, z1*z2 und z1/z2.
| (%i48) |
wxdraw2d( /* Schalte Gitter ein */ grid = true, /* x- und y-Bereich */ xrange = [-3.5,4], yrange = [-1,7.5], /* Stil für den Vektor */ head_length = 0.1, line_type = solid, /* Komplex Zahlen als Vektor */ color = blue, vector([0,0],[realpart(z1),imagpart(z1)]), vector([0,0],[realpart(z2),imagpart(z2)]), color = red, vector([0,0],[realpart(z1*z2),imagpart(z1*z2)]), color = green, vector([0,0],[realpart(z1/z2),imagpart(z1/z2)]) )$ |
| (%i49) |
z1:polarform(z1); z2:polarform(z2); |
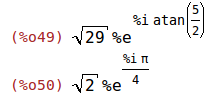
| (%i51) |
z1*z2, %emode:false; z1/z2, %emode:false; |
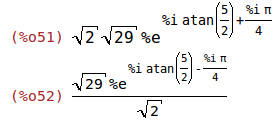
Potenzieren von komplexen Zahlen
Beispiel 3:
Berechnen Sie die folgenden Potenzen mit der Formel von Moivre nach geeigneter Umrechnung der komplexen Zahl in die Polarform.
z1 = (1+i)^3
z2 = (1-i)^5
| (%i53) |
z1: (1+%i)$ z2: (1-%i)$ |
Wir zeigen die Polarform der komplexen Zahlen.
| (%i55) |
polarform(z1); polarform(z2); |

Wir potenzieren die komplexe Zahl in ihrer Polarform und erhalten das Ergebnis in der Polarform.
Hat der Schalter %emode den Wert false, wird für dieses Beispiel die Vereinfachung der Polarform in die Standardform verhindert.
| (%i57) |
polarform(z1)^3, %emode:false; polarform(z2)^5, %emode:false; |

Komplexe Wurzel
Beispiel 4:
Rechnen Sie die komplexen Wurzeln aus den folgenden komplexen Zahlen und skizzieren Sie die Lösungen auf der komplexen Zahlenebene.
z^3 = 1+i
z^4 = 3+i
Wir wählen nicht die übliche Darstellung der komplexen Zahlen in der Polarform um die Wurzeln zu finden. Stattdessen zeigen wir wie mit der Funktion solve die komplexen Lösungen einer Gleichung gefunden werden.
Mit dem Operator "=" wird eine Gleichung definiert. Die Gleichung wird der Variablen eqn1 zugewiesen.
| (%i59) | eqn1: z^3 = 1+%i; |
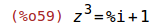
Mit der Funktion solve finden wir die drei Lösungen der Gleichung.
Die Lösungen werden als Gleichungen in einer Liste [] von der Funktion solve zurückgegeben.
| (%i60) | solve(eqn1); |
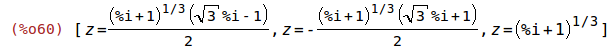
Mit der Funktion rhs können wir die rechte Seite einer Gleichung gewinnen. Die Funktion rhs wird mit der Funktion map auf die Liste angwendet. Das Ergebnis ist wiederum eine Liste, die die gesuchten Lösungen als komplexe Zahlen enthält. Zusätzlich wenden wir noch die Funktion polarform an.
| (%i61) | res1: polarform(map('rhs, %)); |
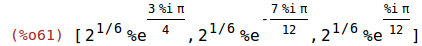
Mit der bereits bekannten Funktion wxdraw2d können wir drei Lösungen in der komplexen Zahlenebene zeichnen.
| (%i62) |
wxdraw2d( /* Schalte Gitter ein */ grid = true, /* x- und y-Bereich */ xrange = [-1.5,1.5], yrange = [-1.5,1.5], /* Stil für den Vektor */ head_length = 0.1, line_type = solid, /* Komplex Zahlen als Vektor */ color = blue, vector([0,0],[realpart(first(res1)), imagpart(first(res1))]), vector([0,0],[realpart(second(res1)),imagpart(second(res1))]), vector([0,0],[realpart(third(res1)), imagpart(third(res1))]) )$ |
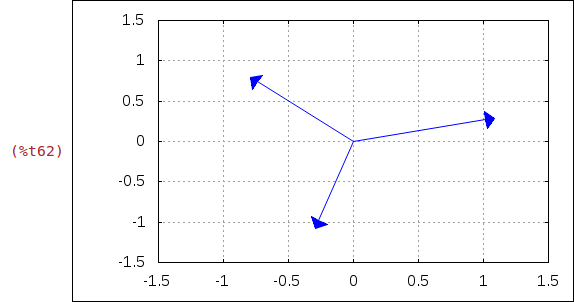
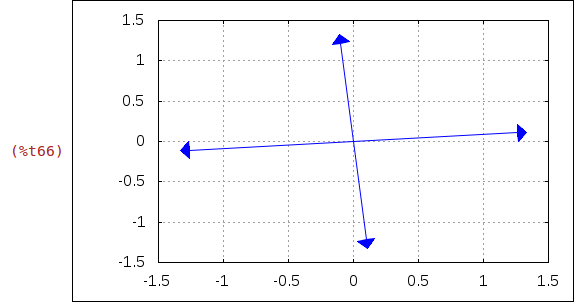
Wir wiederholen die obige Rechnung für ein Beispiel mit vier komplexen Lösungen.
| (%i63) | eqn2: z^4 = 3 + %i; |
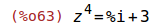
| (%i64) |
solve(eqn2); res2: polarform(map('rhs,%)); |
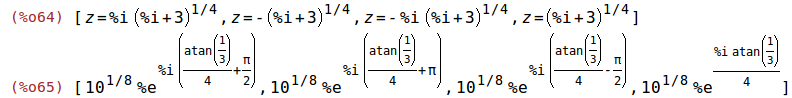
| (%i66) |
wxdraw2d( /* Schalte Gitter ein */ grid = true, /* x- und y-Bereich */ xrange = [-1.5,1.5], yrange = [-1.5,1.5], /* Stil für den Vektor */ head_length = 0.1, line_type = solid, /* Komplex Zahlen als Vektor */ color = blue, vector([0,0],[realpart(first(res2)), imagpart(first(res2))]), vector([0,0],[realpart(second(res2)),imagpart(second(res2))]), vector([0,0],[realpart(third(res2)), imagpart(third(res2))]), vector([0,0],[realpart(fourth(res2)), imagpart(fourth(res2))]) )$ |
Beispiel 5:
a) Bestimmen Sie den Parameter a der komplexen Zahlen so, dass die Produkte rein imaginäre Zahlen ergeben.
| (%i67) | (a+%i)*(3-2*%i)$ |
Wir nehmen den imaginären Anteil und lösen diesen nach dem gesuchten Paramater a mit der Funktion solve auf.
| (%i68) |
imagpart(%); solve(%); |

| (%i70) | (a+2*%i)*(4-3*%i)$ |
| (%i71) |
imagpart(%); solve(%); |

b) Bestimmen Sie den Parameter a der komplexen Zahl so, dass die Produkte rein reelle Zahlen ergeben.
| (%i73) | (2-%i)*(-4+a*%i)$ |
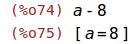
| (%i74) |
realpart(%); solve(%); |
| (%i76) | (a-1/2*%i)*(1+%i)$ |
| (%i77) |
realpart(%); solve(%); |

Beispiel 6:
Berechnen Sie die folgenden komplexen Zahlen und geben Sie die Ergebnisse in der algebraischen und in der Polarform an.
Die Ergebnisse werden mit den Funktionen rectform und polarform berechnet.
| (%i79) | z1: (3-%i)/(3+%i)$ |
| (%i80) | rectform(z1); |
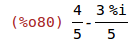
| (%i81) | polarform(z1); |
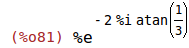
| (%i82) | z2: (sqrt(3)+%i)^36$ |
Für dieses Beispiel erhalten wir kein einfaches Ergebnis mit der Funktion rectform. Wenden wir die ratsimp an, verschwindet der imaginäre Anteil.
| (%i83) |
rectform(z2); ratsimp(%); |
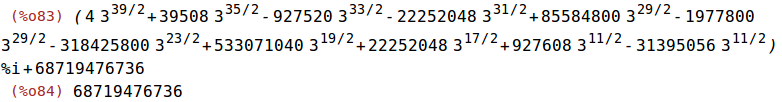
Mit der Funktion polarform erhalten wir für dieses Beispiel sofort ein einfaches Ergebnis.
| (%i85) | polarform(z2); |
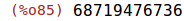
Beispiel 7:
Gegeben ist die komplexe Zahl z = -sqrt(3)/2 + 1/2*%i.
| (%i86) | z: -sqrt(3)/2 + 1/2*%i$ |
a) Berechnen Sie z/i:
| (%i87) | expand(z/%i); |
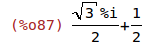
b) Berechnen Sie (z+i)^3:
| (%i88) | ratsimp((z+%i)^3); |

c) Berechnen Sie sqrt(z*i)
| (%i89) | rectform(sqrt(z*%i)); |
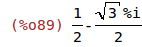
Beispiel 8:
Berechnen Sie die folgenden komplexen Wurzeln.
a) z = (-4+4*%i)^(1/3)
| (%i90) |
kill(z)$ z^3 = (-4+4*%i)$ |
| (%i92) | ratsimp(map('rhs,solve(%))); |
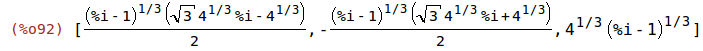
b) z = (-8)^(1/3)
| (%i93) | z^3 = -8$ |
| (%i94) | map('rhs, solve(%)); |
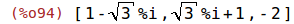
c) z^2 = -1 + sqrt(3)*%i
| (%i95) | z^2 = -1 + sqrt(3)*%i$ |
| (%i96) | map('rhs, solve(%)); |
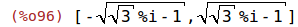
d) z^4 = -1-%i
| (%i97) | z^4 = -1-%i$ |
| (%i98) | map('rhs, solve(%)); |
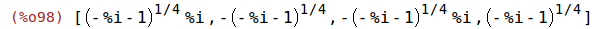
Created with wxMaxima.